Operations of Sets

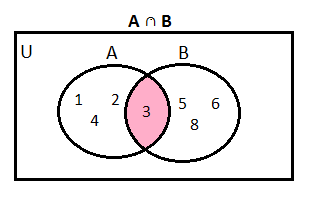
We can perform operations on two given sets such as union of sets, intersection of sets and difference of sets. The operations of sets concept is very important in the field of set theory. Let us see these operations of sets one by one.

Union of Sets

T The union of two sets A and B is a set which consists of all the elements of set A as well as all the elements of set B. It is denoted by A ∪ B and is read as ‘A union B’.

For example, if A = {1, 2, 3, 4} and B = {3, 5, 6, 8}, then A ∪ B = {1, 2, 3, 4, 5, 6, 8}.

Intersection of Sets

The intersection of two sets A and B is a set which consists of elements which are common to both the sets. It is denoted by A ∩ B and is read as ‘A intersection B’.

For example, if A = {1, 2, 3, 4, 5, 6, 7} and B = {1, 3, 5, 7, 9, 11}, then A ∩ B = {1, 3, 5, 7}.

Difference of Sets

If A and B are two sets, then their difference, i.e. A – B is the set of those elements which belong to A but not to B.

Thus, A – B = {x : x ∈ A, x ∉ B} and B – A = {x : x ∈ B, x ∉ A}.

For example, if A = {1, 2, 3, 4, 5} and B = {3, 4, 5}, then A – B = {1, 2} and B – A = φ.

Venn Diagram

Venn diagram was developed by the mathematician John Venn. In these diagrams, the universal set (U) is represented by a rectangle and the sets within are represented by circles.

For example, the given Venn diagram shows set A within the universal set U and A′ is the shaded portion outside the circle known as complement of A.

Suppose U = {17, 18, 19, 20} and A = {19, 20}.

This can be represented by the Venn diagram given alongside.

From the Venn diagram, we observe that, A′ = {17, 18}.

Venn Diagram of Union of Sets

If A = {1, 2, 3, 4} and B = {3, 5, 6, 8}, then A ∪ B = {1, 2, 3, 4, 5, 6, 8}. This can be shown by the Venn diagram as follows:

Venn Diagram of Intersection of Sets

If A = {1, 2, 3, 4} and B = {3, 5, 6, 8}, then A ∩ B = {3}. This can be shown by the Venn diagram as follows:

Venn Diagram of Difference of Sets

If A = {1, 2, 3, 4} and B = {3, 5, 6, 8}, then A – B = {1, 2, 4} and B – A = {5, 6, 8}. These can be shown by the Venn diagram as follows:

Properties of Operations on Sets

Distributive Property

1. If A, B and C are three sets, then A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

This property is called distributive property over the intersection of two sets.

2. If A, B and C are three sets, then the intersection is distributive over union of two sets, i.e., A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

De Morgan’s Laws

If A and B are two sets, then De Morgan’s laws state that:

1. (A ∪ B)′ = A′ ∩ B′

2. (A ∩ B)′ = A′ ∪ B′

To verify the above laws, let us consider an example.

If U = {1, 2, 3, … , 20}, A = {5, 10, 15, 20} and B = {4, 8, 12, 16, 20}, then A ∩ B = {20}

(A ∩ B)′ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19}

A′ = {1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 13, 14, 16, 17, 18, 19}

B′ = {1, 2, 3, 5, 6, 7, 9, 10, 11, 13, 14, 15, 17, 18, 19}

A′ ∪ B′ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19}

∴ (A ∩ B)′ = A′ ∪ B′

Now, A ∪ B = {4, 5, 8, 10, 12, 15, 16, 20}

(A ∪ B)′ = {1, 2, 3, 6, 7, 9, 11, 13, 14, 17, 18, 19}

A′ ∩ B′ = {1, 2, 3, 6, 7, 9, 11, 13, 14, 17, 18, 19}

∴ (A ∪ B)′ = A′ ∩ B′

Cardinal Properties of Sets

1. If A and B are two sets, then n(A ∪ B) = n(A) + n(B) – n(A ∩ B).

If A and B are disjoint sets, then A ∩ B = φ. Hence, n(A ∩ B) = 0.

∴ For disjoint sets, n(A ∪ B) = n(A) + n(B).

2. n(A – B) = n(A ∪ B) – n(B) = n(A) – n(A ∩ B)

3. n(B – A) = n(A ∪ B) – n(A) = n(B) – n(A ∩ B)

4. n(A ∪ B) = n(A – B) + n(B – A) + n(A ∩ B)

5. If universal set (U) is finite and A is any set, then n(A) + n(A′) = n(U)

Example 1: If n(A) = 40, n(B) = 27 and n(A ∩ B) = 15, find

a. n(A ∪ B)

b. n(B – A)

c. n(only B)

Solution:

a. We know that, n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

∴ n(A ∪ B) = 40 + 27 – 15 ⇒ n(A ∪ B) = 52

b. n(B – A) = n(A ∪ B) – n(A) = 52 – 40 = 12

c. n(only B) = n(B – A) = 12

Example 2: If n(A – B) = 12, n(B – A) = 16 and n(A ∩ B) = 5, find

a. n(A)

b. n(B)

c. n(A ∪ B)

Solution:

a. We know that, n(A – B) = n(A) – n(A ∩ B)

∴ 12 = n(A) – 5 ⇒ n(A) = 17

b. We know that, n(B – A) = n(B) – n(A ∩ B)

∴ 16 = n(B) – 5 ⇒ n(B) = 21

c. Again, n(B – A) = n(A ∪ B) – n(A)

∴ 16 = n(A ∪ B) – 17 ⇒ n(A ∪ B) = 33

Operations of Sets