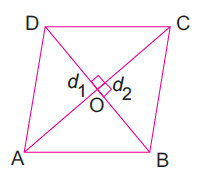
Area of a Rhombus

Area of a Rhombus

 

A rhombus is a special type of parallelogram in which all the sides are equal and the diagonals bisect each other at right angles. To find the area of rhombus, we use the method of splitting the quadrilateral into two triangles.

We know that the area of a triangle = ½ × base × height

Area of rhombus ABCD = Area of ΔABC + Area of ΔADC

                                          = ½ × AC × BO + ½ × AC × DO

                                          = ½ × AC × (BO + DO)

                                          = ½ × AC × BD

                                          = ½ × d₁ × d₂

 

Thus, Area of a rhombus = ½ × d₁ × d₂

Where d₁ and d₂ are the diagonals of the rhombus.

Area of a Rhombus Formula

Area of a rhombus = ½ × d₁ × d₂ 

Where d₁ and d₂ are the diagonals of the rhombus.

Hence, the area of a rhombus is equal to half of the product of its diagonals.

 

If the base and the altitude of a rhombus is given, then we can find the area of a rhombus using the formula of the area of a parallelogram.

Area of a rhombus = b × h

Where b and h are the base and the height of the rhombus, respectively. 

How to Find the Area of a Rhombus When Diagonals are Known  

Consider a rhombus ABCD with two diagonals AC and BD.

• Step 1: Find the length of both the diagonals, d₁ and d₂.
• Step 2: Multiply both the lengths, d₁ and d₂.
• Step 3: Divide the result by 2.

The resultant value will give the area of the rhombus ABCD.

How to Find the Area of a Rhombus When The Base and The Height are Known

Step 1: Note down the lengths of the base and the height of the given rhombus. The base is one of the sides of the rhombus, while the height is the perpendicular distance from the chosen base to the opposite side.

Step 2: Multiply the base and the height.

The resultant value will give the area of the rhombus.

Solved Questions on Area of a Rhombus

Example 1: The lengths of the diagonals of a rhombus are 16 cm and 20 cm. Find its area.

 

Solution: Here, d₁ = 16 cm and d₂ = 20 cm

Area of a rhombus = ½ × d₁ × d₂

                                   = ½ × 16 × 20

                                   = 160 sq. cm

 

Example 2: Find the area of a rhombus, the lengths of whose diagonals are 30 cm and 40 cm.

Solution: Here, d₁ = 30 cm and d₂ = 40 cm

Area of a rhombus = ½ × d₁ × d₂

                                   = ½ × 30 × 40

                                   = 600 sq. cm

 

Example 3: The area of a rhombus is 250 sq. cm. If one of its diagonals is 20 cm long, find the length of the other diagonal.

 

Solution: Here, d₁ = 20 cm and d₂ = ?

Area of a rhombus = 250 sq. cm

Area of a rhombus = ½ × d₁ × d₂

                           250 = ½ × 20 × d₂

                           500 = 20 × d₂

                              d₂ = 500/20 = 25 cm

Hence, the length of the other diagonal is 25 cm.

 

 

Example 4: The perimeter of a rhombus is 40 cm and one of its diagonals is 16 cm. Find the length of the other diagonal. Also, find the area of the rhombus.

 

Solution: Perimeter of the rhombus = 40 cm

Side of the rhombus = 40/4 = 10 cm

In the above figure, AB = BC = CD = AD = 10 cm

Let the diagonal AC = 16 cm

Then, OC = AO = 8 cm

In right-angles triangle AOB,

OB² = AB² – AO²                      [Using Pythagoras theorem]

OB² = 10² – 8²

OB² = 100 – 64

OB² = 36

OB = 6 cm

Thus, the diagonal BD = 12 cm

 

Now, Area of a rhombus = ½ × d₁ × d₂

                                             = ½ × 16 × 12

                                             = 96 sq. cm

Example 5: If the base and the perpendicular height of a rhombus measure 5.5 cm and 4 cm respectively, find the area of the rhombus.

Solution: Here, b = 5.5 cm and h = 4 cm

Area of a rhombus = b × h

                              =  5.5 × 4

                               = 22 sq. cm 

Example 6: The perpendicular height of a rhombus is 6 cm. If the area of the rhombus is 27 sq. cm, find the side of the rhombus.

Solution: Here, h = 6 cm and area = 27 sq. cm

Area of a rhombus = b × h

                          27 =  b × 6

                            b = 27/6 = 4.5 cm 

Thus, each side of the rhombus is 4.5 cm.

To find the area of a trapezium, a parallelogram, a square, a rectangle and a circle, click the following links:

Area of a Trapezium

Area of a Parallelogram

Area of a Square

Area of a Rectangle

Area of a Circle