Surface Area of a Sphere
A sphere is
a three-dimensional (3D) shape which has a curved surface. It has no edges and
no corners. The area occupied by its curved surface is called the surface
area of a sphere. The examples of sphere include football, basketball,
soccer ball, globe, etc.
Let us study
to find the formula to calculate the surface area of a sphere.
We can find
the formula to calculate the surface area of a sphere using the formula to
calculate the surface area of a cylinder.
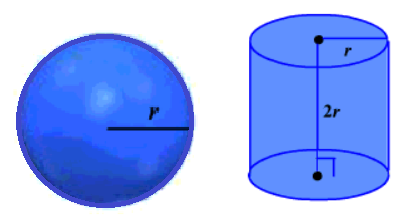
Let us take
a sphere and a cylinder with the same radius and the same height.
If the radius of the sphere is r, then the height of the cylinder, h = 2r as shown in the above figure.
Suppose we
made this cylinder with a paper, then this cylinder is open from top and
bottom. If we open up the cylinder and cover up the sphere with the paper
obtained after opening it, then we see that the paper covers the whole surface
of the sphere. It means that the curved surface area of the cylinder is equal
to the surface area of sphere.
Hence, the
surface area of the sphere = Curved surface area of the cylinder
= 2πrh
Here, the
height of the cylinder, h = 2r
Thus, the
surface area of the sphere = 2πr(2r) = 4πr2
Surface
area of a sphere = 4πr2
Surface Area of a Sphere Formula
Surface
area of a sphere = 4πr2
Surface Area of a Sphere Example
Example
1: Find the surface
area of a sphere whose radius is 7 cm.
Solution: Given: r = 7 cm
Surface area
of a sphere = 4πr2
= 4 × 22/7 × 7 × 7
=
616 sq. cm
Example 2:
How much material is
required to make a football of radius 14 cm.
Solution: Given: r = 14 cm
Surface area
of a sphere = 4πr2
=
4 × 22/7 × 14 × 14
=
2464 sq. cm
Example 3:
If the surface area
of a globe is 9856 sq. cm, find the diameter of the globe.
Solution: Given: Surface area = 9856 sq. cm
Surface area
of a sphere = 4πr2
9856 = 4 × 22/7 × r2
r2
= 68992/88 = 784
r = 28 cm
Diameter = 2r = 2 × 28 = 56 cm