NCERT Solutions for Class 8 Maths Chapter 5 Squares and Square Roots Ex 5.4

NCERT Solutions for Class 8 Maths Chapter 5 Squares and Square Roots Ex 5.4 are the part of NCERT Solutions for Class 8 Maths (Rationalised Contents). Here you can find the NCERT Solutions for Class 8 Maths Chapter 5 Squares and Square Roots Ex 5.4.

NCERT Solutions for Class 8 Maths Chapter 5 Squares and Square Roots Ex 5.1
NCERT Solutions for Class 8 Maths Chapter 5 Squares and Square Roots Ex 5.2
NCERT Solutions for Class 8 Maths Chapter 5 Squares and Square Roots Ex 5.3
NCERT Solutions for Class 8 Maths Chapter 5 Squares and Square Roots Ex 5.4

Ex 5.4 Class 8 Maths Question 1.

Find the square root of each of the following numbers by Division method.
(i) 2304
(ii) 4489
(iii) 3481
(iv) 529
(v) 3249
(vi) 1369
(vii) 5776
(viii) 7921
(ix) 576
(x) 1024
(xi) 3136
(xii) 900

Solution:

Ex 5.4 Class 8 Maths Question 2.

Find the number of digits in the square root of each of the following numbers (without any calculation).
(i) 64
(ii) 144
(iii) 4489
(iv) 27225
(v) 390625

Solution:

Ex 5.4 Class 8 Maths Question 3.

Find the square root of the following decimal numbers.
(i) 2.56
(ii) 7.29
(iii) 51.84
(iv) 42.25
(v) 31.36

Solution:

Ex 5.4 Class 8 Maths Question 4.

Find the least number which must be subtracted from each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 402
(ii) 1989
(iii) 3250
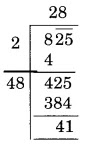
(iv) 825
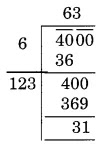
(v) 4000

Solution:
(i)

Here, the remainder is 2.
Thus, 2 is the least number to be subtracted from 402 to get a perfect square.
New square number = 402 – 2 = 400
Thus, √400 = 20

(ii)

Here, the remainder is 53.
Thus, 53 is the least number to be subtracted from 1989 to get a perfect square.
New square number = 1989 – 53 = 1936
Thus, √1936 = 44

(iii)

Here, the remainder is 1.
Thus, 1 is the least number to be subtracted from 3250 to get a perfect square.
New square number = 3250 – 1 = 3249
Thus, √3249 = 57

(iv)

Here, the remainder is 41.
Thus, 41 is the least number to be subtracted from 825 to get a perfect square.
New square number = 825 – 41 = 784
Thus, √784 = 28

(v)

Here, the remainder is 31.
Thus, 31 is the least number to be subtracted from 4000 to get a perfect square.
New square number = 4000 – 31 = 3969
Thus, √3969 = 63

Ex 5.4 Class 8 Maths Question 5.

Find the least number which must be added to each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 525
(ii) 1750
(iii) 252
(iv) 1825
(v) 6412

Solution:
(i)

Here, the remainder is 41.
It represents that the square of 22 is less than 525.
The next square number is 23 and 23² = 529
Hence, the number to be added to 525 to get a perfect square = 529 – 525 = 4
New perfect square number = 529
Thus, √529 = 23

(ii)

Here, the remainder is 69.
It represents that the square of 41 is less than in 1750.
The next square number is 42 and 42² = 1764
Hence, the number to be added to 1750 to get a perfect square = 1764 – 1750 = 14
New perfect square number = 1764
Thus, √1764 = 42

(iii)

Here, the remainder is 27.
It represents that the square of 15 is less than 252.
The next square number is 16 and 16² = 256
Hence, the number to be added to 252 to get a perfect square = 256 – 252 = 4
New perfect square number = 252 + 4 = 256
Thus, √256 = 16

(iv)

Here, the remainder is 61.
It represents that the square of 42 is less than in 1825.
The next square number is 43 and 43² = 1849
Hence, the number to be added to 1825 to get a perfect square = 1849 – 1825 = 24
New perfect square number = 1849

Thus, √1849 = 43

(v)

Here, the remainder is 12.
It represents that the square of 80 is less than 6412.
The next square number is 81 and 81² = 6561
Hence, the number to be added to 6412 to get a perfect square = 6561 – 6412 = 149
New perfect square number = 6561

Thus, √6561 = 81

Ex 5.4 Class 8 Maths Question 6.

Find the length of the side of a square whose area is 441 m².

Solution:
Let the length of each side of the square be x m.
Area of the square = (side)² = x² m²
x² = 441 ⇒ x = √441 = 21

Thus, x = 21 m
Hence, the length of the side of the square is 21 m.

Ex 5.4 Class 8 Maths Question 7.

In a right triangle ABC, ∠B = 90°.
(a) If AB = 6 cm, BC = 8 cm, find AC
(b) If AC = 13 cm, BC = 5 cm, find AB

Solution:
(a) In a right-angled triangle ABC,

AC² = AB² + BC² [By Pythagoras Theorem]

⇒ AC² = (6)² + (8)² = 36 + 64 = 100
⇒ AC = √100 = 10
Thus, AC = 10 cm

(b) In a right-angled triangle ABC,

AC² = AB² + BC² [By Pythagoras Theorem]
⇒ (13)² = AB² + (5)²
⇒ 169 = AB² + 25
⇒ 169 – 25 = AB²
⇒ 144 = AB²
or, AB = √144 = 12 cm
Thus, AB = 12 cm

Ex 5.4 Class 8 Maths Question 8.

A gardener has 1000 plants. He wants to plant these in such a way that the number of rows and the number of columns remain the same. Find the minimum number of plants he needs more for this.

Solution:
Let the number of rows be x. Then the number of columns also be x.
Total number of plants = x × x = x²
x² = 1000 ⇒ x = √1000

Here, the remainder is 39.
So, the square of 31 is less than 1000.
Next square number is 32 and 32² = 1024
Hence, the number to be added to 1000 to get a perfect square = 1024 – 1000 = 24
Thus, the minimum number of plants required by him = 24

Alternative method:

The minimum number of plants required by him = 24.

Ex 5.4 Class 8 Maths Question 9.

There are 500 children in a school. For a P.T. drill, they have to stand in such a manner that the number of rows is equal to the number of columns. How many children would be left out in this arrangement?

Solution:
Let the number of children in a row be x. Then the number of children in a column also be x.
Total number of children = x × x = x²
x² = 500 ⇒ x = √500

Here, the remainder is 16.
New number = 500 – 16 = 484
And, √484 = 22
Thus, 16 children would be left out in this arrangement.

NCERT Solutions for Class 8 Maths Chapter 5 Squares and Square Roots Ex 5.4